在真空中的光滑绝缘水平面上的O点处,固定一个带正电的小球,所带电荷量为Q,直线MN通过O点,N为OM的中点,OM的距离为d.M点处固定一个带负电的小球,所带电荷量为q,质量为m,如图所示.(静电力常量为k)
(1)求N点处的场强大小和方向;
(2)求无初速释放M处的带电小球q时,带电小球的加速度大小;
(3)若点电荷Q所形成的电场中各点的电势的表达式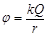 ,其中r为空间某点到点电荷Q的距离.求无初速释放带电小球q后运动到N处时的速度大小v.
,其中r为空间某点到点电荷Q的距离.求无初速释放带电小球q后运动到N处时的速度大小v.
在真空中的光滑绝缘水平面上的O点处,固定一个带正电的小球,所带电荷量为Q,直线MN通过O点,N为OM的中点,OM的距离为d.M点处固定一个带负电的小球,所带电荷量为q,质量为m,如图所示.(静电力常量为k)
(1)求N点处的场强大小和方向;
(2)求无初速释放M处的带电小球q时,带电小球的加速度大小;
(3)若点电荷Q所形成的电场中各点的电势的表达式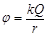 ,其中r为空间某点到点电荷Q的距离.求无初速释放带电小球q后运动到N处时的速度大小v.
,其中r为空间某点到点电荷Q的距离.求无初速释放带电小球q后运动到N处时的速度大小v.