一平板车质量M=50kg，停在水平路面上，车身平板离地面高h=1.25m．一质量m=10kg的小物块置于车的平板上，它到车尾的距离b=1.0m，与平板间的动摩擦因数μ=0.2，如图所示．今对平板车施一水平方向的恒力F=220N，使车由静止向前行驶，经一段时间后物块从平板上滑落，此时车向前行驶的距离x0=2.0m．不计路面与平板车间的摩擦，g取10m/s2．求：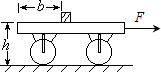
（1）从车开始运动到物块刚离开车所经过的时间t；
（2）物块刚落地时，落地点到车尾的水平距离x．
相关试题
如图所示，物体A重40N，物体B重20N，A与B、B与地面间的动摩擦因数均为0.4，当用水平力向右拉动物体A时，试求：
（1）B物体所受的滑动摩擦力的大小和方向；
（2）A物体所受的地面滑动摩擦力的大小和方向．
如图所示，玻璃棱镜ABCD可以看成是由ADE、ABE、BCD三个直角三棱镜组成。一束频率5.3×1014Hz的单色细光束从AD面入射，在棱镜中的折射光线如图中ab所示，ab与AD面的夹角
。已知光在真空中的速度c=3×108m/s，玻璃的折射率n=1.5，求：
（1）这束入射光线的入射角多大？
（2）光在棱镜中的波长是多大？
（3）该束光线第一次从CD面出射时的折射角。（结果可用三角函数表示）
一简谐横波沿x轴正方向传播，在t=0时刻的波形如图所示.已知介质中质点P的振动周期为2s，此时P质点所在位置的纵坐标为2cm，横坐标为0.5 m.试求从图示时刻开始在哪些时刻质点P会出现在波峰？
粤公网安备 44130202000953号