如图所示,一质量为0.6kg的小物块,静止在光滑水平桌面上,桌面距地面高度为0.8m,用一水平向右的恒力F推动小物块,使物体向右运动,运动2m后撤去恒力F,小物块滑离桌面做平抛运动落到地面,平抛过程的水平位移为0.8m。不计空气阻力,重力加速度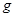 取
取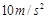 。求:
。求:
(1)小物块飞离桌面时的速度大小;
(2)恒力F的大小。
如图所示,一质量为0.6kg的小物块,静止在光滑水平桌面上,桌面距地面高度为0.8m,用一水平向右的恒力F推动小物块,使物体向右运动,运动2m后撤去恒力F,小物块滑离桌面做平抛运动落到地面,平抛过程的水平位移为0.8m。不计空气阻力,重力加速度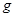 取
取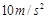 。求:
。求:
(1)小物块飞离桌面时的速度大小;
(2)恒力F的大小。