如图所示,将直径为2R的半圆形导轨固定在竖直面内的A、B两点,直径AB与竖直方向的夹角为60°。在导轨上套一质量为m的小圆环,原长为2R、劲度系数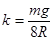 的弹性轻绳穿过圆环且固定在A、B两点。已知弹性轻绳满足胡克定律,形变量相同时弹性势能也相等,且弹性绳始终在弹性限度内,重力加速度为g,不计一切摩擦。将圆环由A点正下方的C点静止释放,当圆环运动到导轨的最低点D点时,求
的弹性轻绳穿过圆环且固定在A、B两点。已知弹性轻绳满足胡克定律,形变量相同时弹性势能也相等,且弹性绳始终在弹性限度内,重力加速度为g,不计一切摩擦。将圆环由A点正下方的C点静止释放,当圆环运动到导轨的最低点D点时,求
(1)圆环的速率v;
(2)导轨对圆环的作用力F的大小?
如图所示,将直径为2R的半圆形导轨固定在竖直面内的A、B两点,直径AB与竖直方向的夹角为60°。在导轨上套一质量为m的小圆环,原长为2R、劲度系数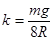 的弹性轻绳穿过圆环且固定在A、B两点。已知弹性轻绳满足胡克定律,形变量相同时弹性势能也相等,且弹性绳始终在弹性限度内,重力加速度为g,不计一切摩擦。将圆环由A点正下方的C点静止释放,当圆环运动到导轨的最低点D点时,求
的弹性轻绳穿过圆环且固定在A、B两点。已知弹性轻绳满足胡克定律,形变量相同时弹性势能也相等,且弹性绳始终在弹性限度内,重力加速度为g,不计一切摩擦。将圆环由A点正下方的C点静止释放,当圆环运动到导轨的最低点D点时,求
(1)圆环的速率v;
(2)导轨对圆环的作用力F的大小?