如图,一透明球体置于空气中,球半径R=10cm,折射率n= .MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN间距为5
.MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN间距为5 cm,CD为出射光线.
cm,CD为出射光线.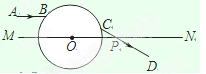
(1)补全光路并求出光从B点传到C点的时间;
(2)求CD与MN所成的角α.(写出求解过程)
如图,一透明球体置于空气中,球半径R=10cm,折射率n= .MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN间距为5
.MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN间距为5 cm,CD为出射光线.
cm,CD为出射光线.
(1)补全光路并求出光从B点传到C点的时间;
(2)求CD与MN所成的角α.(写出求解过程)