如图所示,正方形金属线圈处在磁感应强度B=0.4T的匀强磁场区域内,磁场的方向与线圈平面垂直.金属线圈所围的面积S=100 cm2,匝数n=100,线圈电阻r=1.0 Ω.线圈与电阻R构成闭合回路,电阻的阻值R=3.0 Ω,当线圈从图示位置开始绕中心轴OO′按顺时针方向以角速度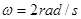 匀速转动时,求:
匀速转动时,求:
(1)线圈转动时产生交变电流的瞬时值表达式;
(2)线圈转动半周,通过电阻R的电量q;
(3)线圈转动半周,电阻R产生的热量QR .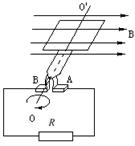
相关知识点
如图所示,正方形金属线圈处在磁感应强度B=0.4T的匀强磁场区域内,磁场的方向与线圈平面垂直.金属线圈所围的面积S=100 cm2,匝数n=100,线圈电阻r=1.0 Ω.线圈与电阻R构成闭合回路,电阻的阻值R=3.0 Ω,当线圈从图示位置开始绕中心轴OO′按顺时针方向以角速度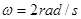 匀速转动时,求:
匀速转动时,求:
(1)线圈转动时产生交变电流的瞬时值表达式;
(2)线圈转动半周,通过电阻R的电量q;
(3)线圈转动半周,电阻R产生的热量QR .