将金属块m用压缩的轻弹簧卡在一个矩形的箱中,如图所示,在箱的上顶板和下底板装有压力传感器,箱可以沿竖直轨道运动,金属块始终没有离开上顶板。当箱以a="2.0" m/s2的加速度竖直向上做匀减速运动时,上顶板的压力显示压力为6.0 N,下底板的压力传感器显示的压力为10.0 N。(g="10" m/s2)
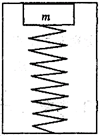
(1)金属块的重力多大?
(2)若上顶板压力传感器的示数是下底板压力传感器的示数的0.4倍,试求箱的加速度大小和方向。
(3)要使上顶板压力传感器的示数为零,箱沿竖直方向运动的情况可能是怎样的?