如图所示,在两端封闭粗细均匀的竖直长管道内,用一可自由移动的活塞A封闭体积相等的两部分气体。开始时管道内气体温度都为T0 =" 500" K,下部分气体的压强P0=1.25×105 Pa,活塞质量m =" 0.25" kg,管道的内径横截面积S =1cm2。现保持管道下部分气体温度不变,上部分气体温度缓慢降至T,最终管道内上部分气体体积变为原来的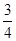 ,若不计活塞与管道壁间的摩擦,g =" 10" m/s2,求此时上部分气体的温度T。
,若不计活塞与管道壁间的摩擦,g =" 10" m/s2,求此时上部分气体的温度T。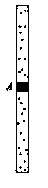
如图所示,在两端封闭粗细均匀的竖直长管道内,用一可自由移动的活塞A封闭体积相等的两部分气体。开始时管道内气体温度都为T0 =" 500" K,下部分气体的压强P0=1.25×105 Pa,活塞质量m =" 0.25" kg,管道的内径横截面积S =1cm2。现保持管道下部分气体温度不变,上部分气体温度缓慢降至T,最终管道内上部分气体体积变为原来的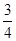 ,若不计活塞与管道壁间的摩擦,g =" 10" m/s2,求此时上部分气体的温度T。
,若不计活塞与管道壁间的摩擦,g =" 10" m/s2,求此时上部分气体的温度T。