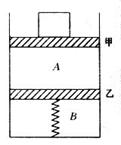
如图所示,一端封闭一端开口粗细均匀的绝热玻璃管的横截面积为10cm2,管内有两个重力不计的活塞,导热活塞甲封闭了长30cm的气柱A,绝热活塞乙用一根劲度系数 、原长为15cm的轻质弹簧和管底相连,气柱B长15cm,气体的初始温度为27℃,现在甲活塞上放一个2kg的砝码,待活塞稳定后再加热气体B,求当气体B的温度升高多少时,活塞甲可返回原处?(大气压
、原长为15cm的轻质弹簧和管底相连,气柱B长15cm,气体的初始温度为27℃,现在甲活塞上放一个2kg的砝码,待活塞稳定后再加热气体B,求当气体B的温度升高多少时,活塞甲可返回原处?(大气压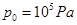 ,摩擦不计,
,摩擦不计, )
)
如图所示,一端封闭一端开口粗细均匀的绝热玻璃管的横截面积为10cm2,管内有两个重力不计的活塞,导热活塞甲封闭了长30cm的气柱A,绝热活塞乙用一根劲度系数 、原长为15cm的轻质弹簧和管底相连,气柱B长15cm,气体的初始温度为27℃,现在甲活塞上放一个2kg的砝码,待活塞稳定后再加热气体B,求当气体B的温度升高多少时,活塞甲可返回原处?(大气压
、原长为15cm的轻质弹簧和管底相连,气柱B长15cm,气体的初始温度为27℃,现在甲活塞上放一个2kg的砝码,待活塞稳定后再加热气体B,求当气体B的温度升高多少时,活塞甲可返回原处?(大气压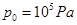 ,摩擦不计,
,摩擦不计, )
)