如图所示，一个小球以v0＝8.0 m/s速度从圆弧轨道的O点水平抛出，恰好能沿着斜面所在的方向落在Q点。已知斜面光滑，斜面与水平面的夹角为θ＝37°，斜面的高度为h＝15 m．忽略空气阻力的影响，重力加速度为g＝10 m/s2。求小球从O点抛出到斜面底端的M点所用的总时间。（保留两位有效数字）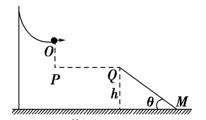
如图所示，一个小球以v0＝8.0 m/s速度从圆弧轨道的O点水平抛出，恰好能沿着斜面所在的方向落在Q点。已知斜面光滑，斜面与水平面的夹角为θ＝37°，斜面的高度为h＝15 m．忽略空气阻力的影响，重力加速度为g＝10 m/s2。求小球从O点抛出到斜面底端的M点所用的总时间。（保留两位有效数字）
÷（ －
）＋0.4×（－
（2）
（2）
=_____________________
粤公网安备 44130202000953号