如图所示为用某种透明材料制成的一块柱形棱镜的截面图,圆弧CD为半径为R的四分之一的圆周,圆心为O,光线从AB面上的某点入射,入射角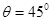 ,它进入棱镜后恰好以临界角射在BC面上的O点。
,它进入棱镜后恰好以临界角射在BC面上的O点。
(a)画出光线由AB面进入棱镜且从CD弧面射出的光路图;
(b)求该棱镜的折射率n;
(c)求光线在该棱镜中传播的速度大小(已知光在空气中的传播速度c=3.0×108m/s)。
如图所示为用某种透明材料制成的一块柱形棱镜的截面图,圆弧CD为半径为R的四分之一的圆周,圆心为O,光线从AB面上的某点入射,入射角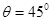 ,它进入棱镜后恰好以临界角射在BC面上的O点。
,它进入棱镜后恰好以临界角射在BC面上的O点。
(a)画出光线由AB面进入棱镜且从CD弧面射出的光路图;
(b)求该棱镜的折射率n;
(c)求光线在该棱镜中传播的速度大小(已知光在空气中的传播速度c=3.0×108m/s)。