如图所示,圆柱形气缸A中用质量为2m的活塞封闭有一定质量的理想气体,温度为27℃,气缸中的活塞通过滑轮系统悬挂一质量为m的重物,稳定时活塞与气缸底部距离为h,现在重物m上加挂质量为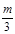 的小物体,已知大气压强为p0,活塞横截面积为S,
的小物体,已知大气压强为p0,活塞横截面积为S,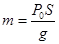 ,不计一切摩擦,求当气体温度升高到37℃且系统重新稳定后,重物m下降的高度。
,不计一切摩擦,求当气体温度升高到37℃且系统重新稳定后,重物m下降的高度。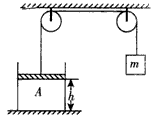
如图所示,圆柱形气缸A中用质量为2m的活塞封闭有一定质量的理想气体,温度为27℃,气缸中的活塞通过滑轮系统悬挂一质量为m的重物,稳定时活塞与气缸底部距离为h,现在重物m上加挂质量为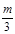 的小物体,已知大气压强为p0,活塞横截面积为S,
的小物体,已知大气压强为p0,活塞横截面积为S,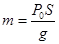 ,不计一切摩擦,求当气体温度升高到37℃且系统重新稳定后,重物m下降的高度。
,不计一切摩擦,求当气体温度升高到37℃且系统重新稳定后,重物m下降的高度。