如图所示,相距3L的AB、CD两直线间的区域存在着两个大小不同、方向相反的有界匀强电场,其中PT上方的电场I的场强方向竖直向下,PT下方的电场II的场强方向竖直向上,电场I的场强大小是电场Ⅱ的场强大小的两倍,在电场左边界AB上有点Q,PQ间距离为L。从某时刻起由Q以初速度v0沿水平方向垂直射入匀强电场的带电粒子,电量为+q、质量为m。通过PT上的某点R进入匀强电场I后从CD边上的M点水平射出,其轨迹如图,若PR两点的距离为2L。不计粒子的重力。试求:

(1)匀强电场I的电场强度E的大小和MT之间的距离;
(2)有一边长为a、由光滑弹性绝缘壁围成的正三角形容器,在其边界正中央开有一小孔S,将其置于CD右侧且紧挨CD边界,若从Q点射入的粒子经AB、CD间的电场从S孔水平射入容器中。欲使粒子在容器中与器壁多次垂直碰撞后仍能从S孔射出(粒子与绝缘壁碰撞时无机械能和电量损失),并返回Q点,需在容器中现加上一个如图所示的匀强磁场,粒子运动的半径小于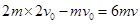 ,求磁感应强度B的大小应满足的条件以及从Q出发再返回到Q所经历的时间。
,求磁感应强度B的大小应满足的条件以及从Q出发再返回到Q所经历的时间。

