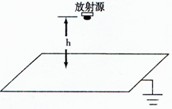
如图所示，在场强为E的竖直向下匀强电场中有一块水平放置的足够大的接地金属板，在金属板的正上方高为h处有一个小的放射源，放射源上方有一铅板，使放射源可以向水平及斜下方各个方向释放质量为m、电量为q、初速度为v0的带电粒子，粒子最后落在金属板上，不计粒子重力．试求：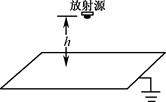
（1）粒子打在板上时的动能；
（2）计算落在金属板上的粒子图形的面积大小．
如图所示，竖直放置的半圆形绝缘轨道半径为R，下端与光滑绝缘水平面平滑连接，整个装置处于方向竖直向上的匀强电场E中．一质量为m、带电量为+q的物块（可视为质点），从水平面上的A点以初速度v0水平向右运动，沿半圆形轨道恰好通过最高点C，场强大小E＜mg/q．
（1）试计算物块在运动过程中克服摩擦力做的功．
（2）证明物块离开轨道落回水平面的水平距离与场强大小E无关，且为一常量．
(10分) 一辆电动自行车的铭牌上给出了如下的技术参数表
| 规格 |
|
后轮驱动直流电机 |
|
| 车型 |
26″电动自行车 |
额定输出功率 |
120W |
| 整车质量 |
30kg |
额定电压 |
40V |
| 最大载量 |
120kg |
额定电流 |
3.5A |
质量为M=70kg的人骑此电动自行车沿平直公路行驶，所受阻力F阻恒为车和人总重的k=0.02倍。g取10m/s2，求：
（1）电机正常工作时的效率。
（2）在电机正常工作时，人骑车行驶的最大速度。
（3）电机以额定功率提供动力的情况下，当车速为v1=1.0m/s时人骑车的加速度。
如图所示，平行带电金属极板A、B间的匀强电场场强E=1.2×103V/m，两极板间的距离d=5cm，电场中C点和D点分别到A、B极板的距离均为0.5cm，C、D间的水平距离L=3cm，B板接地，
求:（1）C、D两点间的电势差UCD；
（2）一带电量q=-2×10—3C的点电荷从C沿直线运动到D的过程中，电荷的电势能变化了多少？
(10分)如图所示的电路中，两平行金属板A、B水平放置，两板间的距离d="40" cm。电源电动势E=24V,内电阻r="1" Ω，电阻R="15" Ω。闭合 开关S， 待电路稳定后，将一带正电的小球从B板小孔以初速度v0="4" m/s竖直向上射入板间。若小球带电量为q=-1×10-2 C,质量为m=2×10-2 kg,不考虑空气阻力。那么，滑动变阻器接入电路的阻值为8Ω时， (取g="10" m/s2)
（1）求滑动变阻器两端电压是多少？电源的输出功率是多少？
（2）带电小球在两板间做什么运动？
(18分)
如图所示,倾角为30°的光滑斜面的下端有一水平传送带,传送带正以6 m/s的速度运动,运动方向如图所示.一个质量为2 kg的物体(物体可以视为质点),从h="3.2" m高处由静止沿斜面下滑,物体经过A点时,不管是从斜面到传送带还是从传送带到斜面,都不计其动能损失.物体与传送带间的动摩擦因数为0.5,物体向左最多能滑到传送带左右两端AB的中点处,重力加速度g="10" m/s2,
则:(1)物体由静止沿斜面下滑到斜面末端需要多长时间?
(2)传送带左右两端AB间的距离L至少为多少?
(3)上述过程中物体与传送带组成的系统产生的摩擦热为多少?
(4)物体随传送带向右运动,最后沿斜面上滑的最大高度h′为多少?
粤公网安备 44130202000953号