如图所示,在空间中取直角坐标系Oxy,在第一象限内平行于y轴的虚线MN与y轴距离为d,从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场,场强大小为E。初速度可以忽略的电子经过另一个电势差为U的电场加速后,从y轴上的A点以平行于x轴的方向射入第一象限区域,A点坐标为(0,h)。已知电子的电量为e,质量为m,加速电场的电势差U>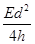 ,电子的重力忽略不计,求:
,电子的重力忽略不计,求:
(1)电子从A点进入电场到离开该电场区域所经历的时间t和离开电场区域时的速度v;
(2)电子经过x轴时离坐标原点O的距离l。
如图所示,在空间中取直角坐标系Oxy,在第一象限内平行于y轴的虚线MN与y轴距离为d,从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场,场强大小为E。初速度可以忽略的电子经过另一个电势差为U的电场加速后,从y轴上的A点以平行于x轴的方向射入第一象限区域,A点坐标为(0,h)。已知电子的电量为e,质量为m,加速电场的电势差U>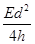 ,电子的重力忽略不计,求:
,电子的重力忽略不计,求:
(1)电子从A点进入电场到离开该电场区域所经历的时间t和离开电场区域时的速度v;
(2)电子经过x轴时离坐标原点O的距离l。