在海滨游乐场里有一种滑沙运动，如图所示。某人坐在滑板上从斜坡的最高处A点由静止开始滑下，滑到斜坡底端B点后，沿水平的滑道再滑行一段距离停下来。若滑板与斜坡滑道和水平滑道间的动摩擦因数均为μ＝0.50，斜坡的倾角θ＝37°，AB长度为25m，斜坡与水平滑道间是平滑连接的，整个运动过程中空气阻力忽略不计，重力加速度g取10m/s2，sin37°＝0.6，cos37°＝0.8。求：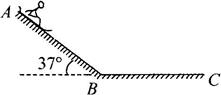
（1）人从斜坡上滑下时的加速度大小；
（2）为保证安全，水平滑道BC的最短长度。
在远距离输电时，如果输送一定的功率，当输电电压为220 V时，在输电线上损失的功率为75 kW；若输电电压提高到6000 V时，在输电线上损耗的功率又是多少?
发电机输出功率为100kW，输出电压是250V，用户需要的电压是220V，发电机到用户输电线电阻为10Ω，要求输电线中因发热而损失的功率为输送功率的4％.
(1)画出此输电线路的示意图；
(2)求输电线路中升压变压器和降压变压器原副线圈的匝数比；
(3)用户得到的电功率是多少。
如下图甲为小型旋转电枢式交流发电机的原理图，其矩形线圈在匀强磁场中绕垂直于磁场方向的固定轴OO′匀速转动，线圈的匝数n＝100、电阻r＝10 Ω，线圈的两端经集流环与电阻R连接，电阻R＝90 Ω，与R并联的交流电压表为理想电表．在t＝0时刻，线圈平面与磁场方向平行，穿过每匝线圈的磁通量Φ随时间t按下图乙所示正弦规律变化．求：
(1)交流发电机产生的电动势最大值；
(2)电路中交流电压表的示数．
如图所示，单匝线圈在匀强磁场中绕
轴从图示位置开匀速转动．已知从图示位置转过
时，线圈中电动势大小为10V，求：
(1)交变电动势的峰值，
(2)交变电动势的有效值；
(3)设线圈电阻为R=1Ω，角速度ω=100rad／s，求线圈由图示位置转过
过程中通过导线截面的电荷量
(4)写出交变电流电动势瞬时值的表达式
粤公网安备 44130202000953号