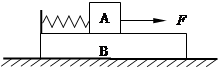
如图所示,质量分别为M、m的两物块A、B通过一轻质弹簧连接,B足够长、放置在水平面上,所有接触面均光滑。弹簧开始时处于原长,运动过程中始终处在弹性限度内。在物块A上施加一个水平恒力F,A、B从静止开始运动,弹簧第一次恢复原长时A、B速度分别为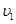 、
、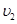 。
。
(1)求物块A加速度为零时,物块B的加速度;
(2)求弹簧第一次恢复原长时,物块B移动的距离;
(3)试分析:在弹簧第一次恢复原长前,弹簧的弹性势能最大时两物块速度之间的关系?简要说明理由。
如图所示,质量分别为M、m的两物块A、B通过一轻质弹簧连接,B足够长、放置在水平面上,所有接触面均光滑。弹簧开始时处于原长,运动过程中始终处在弹性限度内。在物块A上施加一个水平恒力F,A、B从静止开始运动,弹簧第一次恢复原长时A、B速度分别为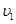 、
、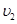 。
。
(1)求物块A加速度为零时,物块B的加速度;
(2)求弹簧第一次恢复原长时,物块B移动的距离;
(3)试分析:在弹簧第一次恢复原长前,弹簧的弹性势能最大时两物块速度之间的关系?简要说明理由。