(11分) 如右图所示的电路中，两平行金属板A、B水平放置，两板间的距离d="40" cm.电路电压恒为U=24V，电阻R=16Ω。闭合开关S，待电路稳定后，将一带正电的小球从B板小孔以初速度v0="4" m/s竖直向上射入板间。若小球带电荷量为q=1×10-2 C，质量为m=2×10-2 kg，不考虑空气阻力。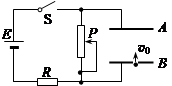
求：（1）滑动变阻器接入电路的阻值为多大时，小球恰能到达A板？
（2）此时滑动变阻器消耗功率是多大？(取g="10" m/s2)
相关试题
如图所示，一不可伸长的轻质细绳，绳长为L一端固定于O点，另一端系一质量为m的小球，小球绕O点在竖直平面内做圆周运动（不计空气助力），小球通过最低点时的速度为v。求小球通过最低点时，绳对小球拉力F的大小；
若小球运动到最低点或最高点时，绳突然断开，两种情况下小球从抛出到落地水平位移大小相等，求O点距地面的高度h;
在(2)中所述情况下试证明O点距离地面高度h与绳长l之间应满足
一斜面AB长为10m，倾角为30°，一质量为2kg的小物体（大小不计）从斜面顶端A点由静止开始下滑，如图所示（g取10 m/s2）
若斜面与物体间的动摩擦因数为0.5，求小物体下滑到斜面底端B点时的速度及所用时间．
3.65m/s
s若给小物体一个沿斜面向下的初速度，恰能沿斜面匀速下滑，则小物体与斜面间的动摩擦因数μ是多少? μ＝0.58
一质点做匀加速直线运动，初速度为10m/s ，加速度为2m/s2 。试求该质点：第5s末的速度20 m/s
前5s内的平均速度15m/s
第5s内的平均速度19m/s
粤公网安备 44130202000953号