如图甲所示,水平光滑的桌面上静止放置一条长为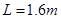 的纸带,纸带上正中间位置放置有一质量为
的纸带,纸带上正中间位置放置有一质量为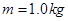 的小铁块,纸带的左边恰好在桌面的左边缘,小铁块与纸带间的动摩擦因数为
的小铁块,纸带的左边恰好在桌面的左边缘,小铁块与纸带间的动摩擦因数为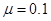 .现让纸带从
.现让纸带从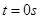 时刻开始一直保持
时刻开始一直保持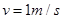 的速度向左匀速运动.已知桌面高度为
的速度向左匀速运动.已知桌面高度为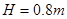 ,
,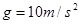 ,小铁块在运动过程中不翻滚,不计空气阻力.求:
,小铁块在运动过程中不翻滚,不计空气阻力.求: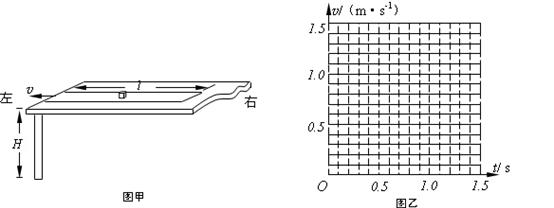
(1)小铁块从开始运动到桌面边缘过程所经历的时间并在乙图画出此过程中小铁块的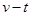 图象;
图象;
(2)小铁块抛出后落地点到抛出点的水平距离;
(3)小铁块从开始运动到桌面边缘过程中产生的内能。
如图甲所示,水平光滑的桌面上静止放置一条长为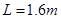 的纸带,纸带上正中间位置放置有一质量为
的纸带,纸带上正中间位置放置有一质量为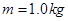 的小铁块,纸带的左边恰好在桌面的左边缘,小铁块与纸带间的动摩擦因数为
的小铁块,纸带的左边恰好在桌面的左边缘,小铁块与纸带间的动摩擦因数为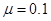 .现让纸带从
.现让纸带从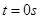 时刻开始一直保持
时刻开始一直保持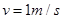 的速度向左匀速运动.已知桌面高度为
的速度向左匀速运动.已知桌面高度为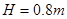 ,
,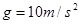 ,小铁块在运动过程中不翻滚,不计空气阻力.求:
,小铁块在运动过程中不翻滚,不计空气阻力.求:
(1)小铁块从开始运动到桌面边缘过程所经历的时间并在乙图画出此过程中小铁块的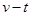 图象;
图象;
(2)小铁块抛出后落地点到抛出点的水平距离;
(3)小铁块从开始运动到桌面边缘过程中产生的内能。