如图所示,两带有等量异种电荷的平行金属板M、N竖直放置,M、N两板间的距离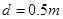 .现将一质量为
.现将一质量为 、电荷量
、电荷量 的带电小球从两极-板上方A点以
的带电小球从两极-板上方A点以 的初速度水平抛出,A点距离两板上端的高度
的初速度水平抛出,A点距离两板上端的高度 ,之后小球恰好从靠近M板上端处进入两板间,沿直线运动碰到N板上的B点,不计空气阻力,取
,之后小球恰好从靠近M板上端处进入两板间,沿直线运动碰到N板上的B点,不计空气阻力,取 .设匀强电场只存在于M、N之间。求:
.设匀强电场只存在于M、N之间。求:
(1)两极板间的电势差.
(2)小球由A到B所用总时间
(3)小球到达B点时的动能.
如图所示,两带有等量异种电荷的平行金属板M、N竖直放置,M、N两板间的距离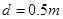 .现将一质量为
.现将一质量为 、电荷量
、电荷量 的带电小球从两极-板上方A点以
的带电小球从两极-板上方A点以 的初速度水平抛出,A点距离两板上端的高度
的初速度水平抛出,A点距离两板上端的高度 ,之后小球恰好从靠近M板上端处进入两板间,沿直线运动碰到N板上的B点,不计空气阻力,取
,之后小球恰好从靠近M板上端处进入两板间,沿直线运动碰到N板上的B点,不计空气阻力,取 .设匀强电场只存在于M、N之间。求:
.设匀强电场只存在于M、N之间。求:
(1)两极板间的电势差.
(2)小球由A到B所用总时间
(3)小球到达B点时的动能.