如图所示,置于圆形水平转台边缘的小物块随转台加速转动,当转速达到某一数值时,物块恰好滑离转台开始做平抛运动.现测得转台半径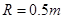 ,离水平地面的高度
,离水平地面的高度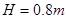 ,物块平抛落地过程水平位移的大小
,物块平抛落地过程水平位移的大小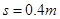 .设物体所受的最大静摩擦力等于滑动摩擦力,取重力加速度
.设物体所受的最大静摩擦力等于滑动摩擦力,取重力加速度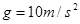 .求:
.求: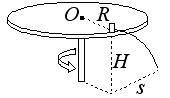
(1)物块做平抛运动的初速度大小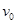 ;(2)物块与转台间的动摩擦因数
;(2)物块与转台间的动摩擦因数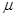 .
.
如图所示,置于圆形水平转台边缘的小物块随转台加速转动,当转速达到某一数值时,物块恰好滑离转台开始做平抛运动.现测得转台半径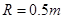 ,离水平地面的高度
,离水平地面的高度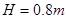 ,物块平抛落地过程水平位移的大小
,物块平抛落地过程水平位移的大小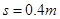 .设物体所受的最大静摩擦力等于滑动摩擦力,取重力加速度
.设物体所受的最大静摩擦力等于滑动摩擦力,取重力加速度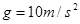 .求:
.求:
(1)物块做平抛运动的初速度大小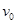 ;(2)物块与转台间的动摩擦因数
;(2)物块与转台间的动摩擦因数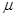 .
.