一只乒乓球质量为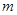 ,从离桌面高为
,从离桌面高为 处由静止释放,假设它与桌面碰撞反弹时不损失机械能,但由于受到大小不变的空气阻力的影响(空气浮力不计),每次反弹的高度是它下落时高度的
处由静止释放,假设它与桌面碰撞反弹时不损失机械能,但由于受到大小不变的空气阻力的影响(空气浮力不计),每次反弹的高度是它下落时高度的 。求:
。求:
(1)空气阻力的大小;
(2)它停止运动前通过的总路程;
(3)为使乒乓球每次都能返回到 高处,每当它到达
高处,每当它到达 高处时,应给它多大的动能?
高处时,应给它多大的动能?
一只乒乓球质量为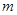 ,从离桌面高为
,从离桌面高为 处由静止释放,假设它与桌面碰撞反弹时不损失机械能,但由于受到大小不变的空气阻力的影响(空气浮力不计),每次反弹的高度是它下落时高度的
处由静止释放,假设它与桌面碰撞反弹时不损失机械能,但由于受到大小不变的空气阻力的影响(空气浮力不计),每次反弹的高度是它下落时高度的 。求:
。求:
(1)空气阻力的大小;
(2)它停止运动前通过的总路程;
(3)为使乒乓球每次都能返回到 高处,每当它到达
高处,每当它到达 高处时,应给它多大的动能?
高处时,应给它多大的动能?