一个密闭的气缸内的理想气体被活塞分成体积相等的左右两室，气缸

更新 2022-09-03
科目物理
题型计算题
难度中等
浏览 1055

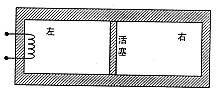
一个密闭的气缸内的理想气体被活塞分成体积相等的左右两室，气缸壁与活塞都是不导热的，活塞与气缸壁之间没有摩擦。开始时，左右两室中气体的温度相等，如图所示。现利用左室中的电热丝对左室中的气体加热一段时间。达到平衡后，左室气体的体积变为原来体积的1．5倍，且右室气体的温度变为300 K。求加热后左室气体的温度。（忽略气缸、活塞的热胀冷缩）

登录免费查看答案和解析

相关试题

如图所示，两块相同平板 $P_{1}$ 、 $P_{2}$ 置于光滑水平面上，质量均为 $m$ 。 $P_{2}$ 的右端固定一轻质弹簧，左端 $A$ 与弹簧的自由端 $B$ 相距 $L$ 。物体 $P$ 置于 $P_{1}$ 的最右端，质量为 $2 m$ 且可以看作质点。 $P_{1}$ 与 $P$ 以共同速度 $v_{0}$ 向右运动，与静止的 $P_{2}$ 发生碰撞，碰撞时间极短，碰撞后 $P_{1}$ 与 $P_{2}$ 粘连在一起， $P$ 压缩弹簧后被弹回并停在A点（弹簧始终在弹性限度内）。 $P$ 与 $P_{2}$ 之间的动摩擦因数为 $μ$ ，求：

（1） $P_{1}$ 、 $P_{2}$ 刚碰完时的共同速度 $v_{1}$ 和 $P$ 的最终速度 $v_{2}$ ；

（2）此过程中弹簧最大压缩量 $x$ 和相应的弹性势能 $E_{p}$ 。

题型：未知
难度：未知

收藏答案/解析

如图甲所示，空间存在一范围足够大的垂直于 $x O y$ 平面向外的匀强磁场，磁感应强度大小为 $B$ 。让质量为 $m$ ，电荷量为 $q (q > 0)$ 的粒子从坐标原点 $O$ 沿 $x O y$ 平面以不同的初速度大小和方向入射到磁场中。不计重力和粒子间的影响。

（1）若粒子以初速度 $v_{1}$ 沿 $y$ 轴正向入射，恰好能经过 $x$ 轴上的 $A (a, 0)$ 点，求 $v_{1}$ 的大小；
（2）已知一粒子的初速度大小为 $v (v ＞ v_{1})$ ，为使该粒子能经过 $A (a, 0)$ 点，其入射角 $θ$ （粒子初速度与 $x$ 轴正向的夹角）有几个？并求出对应的 $\sin θ$ 值；
（3）如图乙，若在此空间再加入沿 $y$ 轴正向、大小为 $E$ 的匀强电场，一粒子从 $O$ 点以初速度 $v_{0}$ 沿 $y$ 轴正向发射。研究表明：粒子在 $x O y$ 平面内做周期性运动，且在任一时刻，粒子速度的 $x$ 分量 $v_{x}$ 与其所在位置的 $y$ 坐标成正比，比例系数与场强大小 $E$ 无关。求该粒子运动过程中的最大速度值 $v_{m}$ 。 $(q > 0)$

题型：未知
难度：未知

收藏答案/解析

质量为 $M$ 、长为 $\sqrt{3} L$ 的杆水平放置，杆两端 $A$ 、 $B$ 系着长为3 $L$ 的不可伸长且光滑的柔软绳，绳上套着一质量为 $m$ 的小铁环。已知重力加速度为 $g$ ，不计空气影响。

（1）现让杆和环均静止悬挂在空中，如图甲，求绳中拉力的大小；
（2）若杆与环保持相对静止，在空中沿 $A B$ 方向水平向右做匀加速直线运动，此时环恰好悬于 $A$ 端的正下方，如图乙所示。
①求此状态下杆的加速度大小 $a$ ；
②为保持这种状态需在杆上施加一个多大的外力，方向如何？

题型：未知
难度：未知

收藏答案/解析

如图所示，一不可伸长的轻绳上端悬挂于 $O$ 点，下端系一质量 $m = 1.0 k g$ 的小球。现将小球拉到 $A$ 点（保持绳绷直）由静止释放，当它经过 $B$ 点时绳恰好被拉断，小球平抛后落在水平地面上的 $C$ 点。地面上的D点与 $O B$ 在同一竖直线上，已知绳长 $L = 1.0 m$ ， $B$ 点离地高度 $H = 1.0 m$ ， $A$ 、 $B$ 两点的高度差 $h = 0.5 m$ ，重力加速度 $g$ 取 $10 m / s^{2}$ ，不计空气阻力影响，求：

（1）地面上 $D C$ 两点间的距离 $s$ ；

（2）轻绳所受的最大拉力大小。

题型：未知
难度：未知

收藏答案/解析

如图所示，O点离地面高度为H，以O点为圆心，制作一个半径为R的四分之一光滑圆弧轨道，小球从与O点等高的圆弧最高点A从静止滚下，并从B点水平抛出，试求：

（1）小球落地点到O点的水平距离.
（2）要使这一距离最大，应满足什么条件?最大距离为多少?

题型：未知
难度：未知

收藏答案/解析