如图所示的匀强电场中,有a、b、c三点,ab间距离Lab=6cm,bc间距离Lbc=10cm,其中ab沿电场方向,bc和电场方向成60°角。一个带电量q=-4×10-8的负电荷从b点移到c点克服电场力做功2×10-6。求: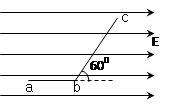
(1)匀强电场的电场强度为多大;
(2)该电荷从a点移到b点,该电荷的电势能的变化量;
(3)a、c两点间的电势差。
如图所示的匀强电场中,有a、b、c三点,ab间距离Lab=6cm,bc间距离Lbc=10cm,其中ab沿电场方向,bc和电场方向成60°角。一个带电量q=-4×10-8的负电荷从b点移到c点克服电场力做功2×10-6。求: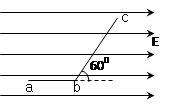
(1)匀强电场的电场强度为多大;
(2)该电荷从a点移到b点,该电荷的电势能的变化量;
(3)a、c两点间的电势差。