粗糙的水平面上放置一质量为m =" 1.2" kg的小物块(可视为质点),对它施加F =" 3" N的水平作用力,使物块沿水平面向右匀加速运动.已知物块通过A点时的速度为vA =" 1" m/s,到达B点所用时间t1 =" 2" s,此后再运动x =" 8" m到达C点,到C点的速度为vC =" 5" m/s,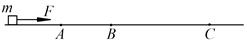
求:(1)物块在水平面上运动的加速度a
(2)物块与水平面间的动摩擦因数μ
粗糙的水平面上放置一质量为m =" 1.2" kg的小物块(可视为质点),对它施加F =" 3" N的水平作用力,使物块沿水平面向右匀加速运动.已知物块通过A点时的速度为vA =" 1" m/s,到达B点所用时间t1 =" 2" s,此后再运动x =" 8" m到达C点,到C点的速度为vC =" 5" m/s,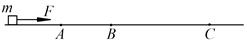
求:(1)物块在水平面上运动的加速度a
(2)物块与水平面间的动摩擦因数μ