如图所示，真空中的矩形abcd区域内存在竖直向下的匀强电场，半径为R的圆形区域内同时存在垂直于纸面向里的匀强磁场，磁感应强度为B，圆形边界分别相切于ad、bc边的中点e、f。一带电粒子以初速度v0沿着ef方向射入该区域后能做直线运动；当撤去磁场并保留电场，粒子以相同的初速度沿着ef方向射入恰能从c点飞离该区域。已知
，忽略粒子的重力。求：
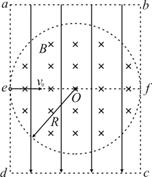
（1）带电粒子的电荷量q与质量m的比值
；
（2）若撤去电场保留磁场，粒子离开矩形区域时的位置。
如图，A、B、C三板平行，B板延长线与圆切于P点， C板与圆切于Q点。离子源产生的初速为零、带电量为q、质量为m的正离子被电压为U0的加速电场加速后沿两板间中点垂直射入匀强偏转电场，偏转后恰从B板边缘离开电场，经过一段匀速直线运动，进入半径为r的圆形匀强磁场，偏转后垂直C板打在Q点。（忽略粒子所受重力）（
，
，偏转电场极板长
、板间距
，
）求：
（1）偏转电压U；
（2）粒子进入磁场时速度的大小及速度与B板的夹角；
（3）磁感应强度B的大小。
如图甲所示，均匀的金属圆环环面积s=0.5m2，电阻r=0.1Ω，环上开一小口，用不计电阻的导线接一R=0.4Ω的电阻。与环同心的圆形区域内有垂直与环平面的匀强磁场，当磁场的磁感应强度B按图乙所示规律变化时（规定磁场垂直环面向外时B为正），求:
(1).环上感应电动势的大小； (2).A、B两点的电势差
； (3).在0~4s内，通过R的电量
.
在如图所示的直角坐标中，x轴的上方有与x轴正方向成θ=45°角的匀强电场，场强的大小为
。x轴的下方有垂直于xOy面的匀强磁场，磁感应强度的大小为B＝2×10－2T，方向垂直纸面向外。把一个比荷为
的带正电粒子从坐标为（0，1.0）的A点处由静止释放，电荷所受的重力忽略不计。求:
（1）带电粒子从释放到第一次进入磁场时所用的时间t；
（2）带电粒子在磁场中的偏转半径R；
（3）带电粒子第三次到达x轴上的位置坐标。
如图所示，匀强电场场强E=4V/m，方向水平向左，匀强磁场的磁感应强度B=2T，方向垂直纸面向里。质量m=1kg的带正电小物体A，从M点沿粗糙、绝缘的竖直墙壁无初速下滑，它滑行h=0.8m到N点时脱离墙壁做曲线运动，在通过P点瞬时，A受力平衡，此时其速度与水平方向成θ=45°角，且P点与M点的高度差为H=1.6m，当地重力加速度g取10m/s2。求：
（1）A沿墙壁下滑时，克服摩擦力做的功Wf；
（2）P点与M点的水平距离s。
粤公网安备 44130202000953号