为满足不同列车间车厢进行重新组合的需要,通常需要将相关的列车通过“驼峰”送入编组场后进行重组(如图所示),重组后的车厢同一组的分布在同一轨道上,但需要挂接在一起。现有一列火车共有 n节车厢,需要在编好组的“驼峰”左侧逐一撞接在一起。已知各车厢之间间隙均为s0,每节车厢的质量都相等,现有质量与车厢质量相等、且没有动力驱动的机车经过“驼峰”以速度v0向第一节车厢运动,碰撞后通过“詹天佑挂钩”连接在一起,再共同去撞击第二节车厢,直到 n 节全部挂好。不计车厢在挂接中所受到的阻力及碰撞过程所需的时间,求:
(1)这列火车的挂接结束时速度的大小;
(2)机车带动第一节车厢完成整个撞接过程所经历的时间。
(3)这列火车完成所有车厢挂接后,机车立即开启动力驱动,功率恒为P,在行驶中的阻力f恒定,经历时间t达到最大速度,求机车此过程的位移。

 ,皮带在电动机的带动下,始终保持
,皮带在电动机的带动下,始终保持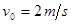 的速率运行。现把一质量为
的速率运行。现把一质量为 的工件(可看为质点)轻轻放在皮带的底端,经时间1.9s,工件被传送到h=1.5m的高处,取g=10m/s2。求:
的工件(可看为质点)轻轻放在皮带的底端,经时间1.9s,工件被传送到h=1.5m的高处,取g=10m/s2。求:
 ,传送带以
,传送带以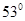 角保持不变,如图所示,这时小朋友拉住线的力为T=10N,(g取10m/s2,不计风筝所受的浮力)求:
角保持不变,如图所示,这时小朋友拉住线的力为T=10N,(g取10m/s2,不计风筝所受的浮力)求:
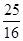 m/s2的加速度做匀加速运动,后以最大行驶速度25 m/s匀速运动,追赶前方以15 m/s的速度同向匀速行驶的卡车.已知摩托车开始运动时与卡车的距离为1000 m,则:
m/s2的加速度做匀加速运动,后以最大行驶速度25 m/s匀速运动,追赶前方以15 m/s的速度同向匀速行驶的卡车.已知摩托车开始运动时与卡车的距离为1000 m,则: 粤公网安备 44130202000953号
粤公网安备 44130202000953号