如图所示，质量为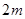
的木板A静止在光滑水平面上，其右端与固定挡板相距
，内壁光滑的弹射器利用压缩弹簧把质量为
的物块B（视为质点）水平向右弹射出去，B弹出后从A左端的上表面水平滑入，之后立刻拿走弹射器。已知A足够长，B不会从A表面滑出，A与挡板的碰撞无机械能损失；弹射器弹簧储存的弹性势能为
，重力加速度为
，不计空气阻力。
（1）B从A左端的上表面水平滑入时的初速度大小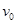
（2）若A与挡板碰撞前，A、B已相对静止，求A碰撞挡板前的速度
（3）若A与挡板只发生一次碰撞，求A、B之间的动摩擦因数
满足的条件。
如图所示，AB为1/4圆弧轨道，半径为R=0.8m，BC是水平轨道，长S=3m，BC处的摩擦系数为μ=1/15，今有质量m=1kg的物体，自A点从静止起下滑到C点刚好停止。求：
（1）物体在AB段克服阻力所做的功为多少？
（2）物体下滑到B点时对圆弧轨道的压力多大？
一辆值勤的警车停在公路边，当警员发现从他旁边以10m/s的速度匀速行驶的货车严重超载时，决定前去追赶，经过5.5s后警车发动起来，并以2.5m/s2的加速度做匀加速运动，但警车的行驶速度必须控制在90km/h以内．问：
（1）警车在追赶货车的过程中，两车间的最大距离是多少；
（2）警车发动后要多长时间才能追上货车.
如图所示，A、B两物体叠放在水平地面上，已知A、B的质量分别为m A=20kg,mB=10kg,A、B之间，B与地面之间的动摩擦因数均为μ=0.5,一轻绳一端系住物体A，另一端固定在墙上，绳与竖直方向的夹角为370，今欲用外力F将物体B匀速向右拉出，(取g=10m/s2,sin370=0.6,cos370=0.8)求：
（1）轻绳对A的拉力大小
（2）水平外力F的大小
一光滑圆环固定在竖直平面内，环上套着一个中央有孔的小球，球静止在圆环上的A点，圆环的圆心为O，OA与水平方向的夹角为600，小球质量为4kg,球与圆环间的动 摩擦因数为0.7，取g=10m/s2
求：（1）球对环的压力；
（2）球受到的摩擦力大小
粤公网安备 44130202000953号