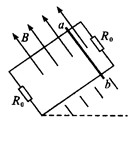
如图所示,一平面框架与水平面成37°角,宽L=0.4m,上、下两端各有一个电阻R0=1Ω,框架的其他部分电阻不计,框架足够长.垂直于框平面的方向存在向上的匀强磁场,磁感应强度B=2T。ab为金属杆,其长度为L=0.4m,质量m=0.8kg,电阻r=0.5Ω,金属杆与框架的动摩擦因数μ=0.5。金属杆由静止开始下滑,直到速度达到最大的过程中,金属杆克服磁场力所做的功为W=1.5J。已知sin37°=0.6,cos37°=0.8;g取10m/s2.求:
(1)ab杆达到的最大速度v.
(2)ab杆从开始到速度最大的过程中沿斜面下滑的距离.
(3)在该过程中通过ab的电荷量.