特种兵过山谷的一种方法可简化为如图所示的模型:将一根长不可伸长的细绳的两端固定在相距为d的A、B两等髙处,细绳上有小滑轮P,战士们相互配合,可沿着细绳滑到对面。开始时,战士甲拉住滑轮,质量为m的战士乙吊在滑轮上,处于静止状态,AP沿竖直方向,且大小等于 d。(不计滑轮与绳的质量,不计滑轮的大小及摩擦,重力加速度为g)若甲对滑轮的拉力沿水平方向,求拉力的大小。
d。(不计滑轮与绳的质量,不计滑轮的大小及摩擦,重力加速度为g)若甲对滑轮的拉力沿水平方向,求拉力的大小。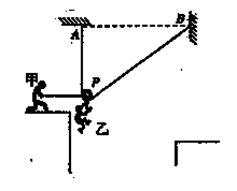
特种兵过山谷的一种方法可简化为如图所示的模型:将一根长不可伸长的细绳的两端固定在相距为d的A、B两等髙处,细绳上有小滑轮P,战士们相互配合,可沿着细绳滑到对面。开始时,战士甲拉住滑轮,质量为m的战士乙吊在滑轮上,处于静止状态,AP沿竖直方向,且大小等于 d。(不计滑轮与绳的质量,不计滑轮的大小及摩擦,重力加速度为g)若甲对滑轮的拉力沿水平方向,求拉力的大小。
d。(不计滑轮与绳的质量,不计滑轮的大小及摩擦,重力加速度为g)若甲对滑轮的拉力沿水平方向,求拉力的大小。