如图所示，三个台阶每个台阶高h=0.225m，宽s=0.3m。小球在平台AB上以初速度v0水平向右滑出，要使小球正好落在第2个平台CD上，不计空气阻力，求初速v0范围。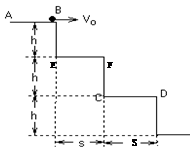
某同学计算如下：(g取10m/s2)根据平抛规律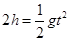
，
到达D点小球的初速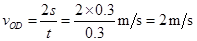 
到达C点小球的初速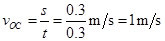 
所以落到台阶CD小球的初速范围是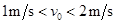 
以上求解过程是否有问题，若有，指出问题所在，并给出正确的解答。
相关试题
如图所示，三个台阶每个台阶高h=0.225m，宽s=0.3m。小球在平台AB上以初速度v0水平向右滑出，要使小球正好落在第2个平台CD上，不计空气阻力，求初速v0范围。
某同学计算如下：(g取10m/s2)根据平抛规律，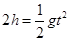
到达D点小球的初速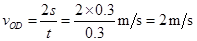
到达C点小球的初速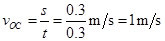
所以落到台阶CD小球的初速范围是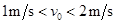
以上求解过程是否有问题，若有，指出问题所在，并给出正确的解答。
.求爆炸中释放的能量．
c，它们的相对速度是多少？在实验室中观测，每个电子的质量是多少？(本题计算结果中的光速c和电子的静质量me不必代入数值．)
粤公网安备 44130202000953号