在光滑的水平面上，用一根轻绳系一个质量为3千克小球，以10m/s速度做匀速圆周运动，半径为4m，若运动到A点，突然把绳再放长4米，绳绷紧后小球转入另一轨道上做匀速圆周运动，求: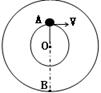
（1）小球从放绳开始到运动到O点的另一侧与AO共线的B点所需的时间。
（2）在B点绳子所受的拉力。
图1是交流发电机模型示意图。在磁感应强度为B的匀强磁场中，有一矩形线圈可绕线圈平面内垂直于磁感线的轴
转动，由线圈引起的导线和
分别与两个跟线圈一起绕
转动的金属圈环相连接，金属圆环又分别与两个固定的电刷保持滑动接触，这样矩形线圈在转动中就可以保持和外电路电阻R形成闭合电路。图2是线圈的主视图，导线分别用它们的横截面来表示。已知
长度为
，
长度为
，线圈以恒定角速度
逆时针转动。（只考虑单匝线圈）
（1）线圈平面处于中性面位置时开始计时，试推导时刻整个线圈中的感应电动势
的表达式；
（2）线圈平面处于与中性面成夹角位置时开始计时，如图3所示，试写出
时刻整个线圈中的感应电动势
的表达式；
（3）若线圈电阻为，求线圈每转动一周电阻
上产生的焦耳热。（其它电阻均不计）
质量为的弹性球从空中某高度由静止开始下落，该下落过程对应的
图象如图所示。球与水平地面相碰后离开地面时的速度大小为碰撞前的
。设球受到的空气阻力大小恒为
，取
, 求：
（1）弹性球受到的空气阻力的大小；
（2）弹性球第一次碰撞后反弹的高度。
如图所示，光滑水平面上有两辆车，甲车上面有发射装置，甲车连同发射装置质量M1=1kg，车上另有一个质量为m=0.2kg的小球。甲车静止在平面上， 乙车以V0=8m/s的速度向甲车运动，乙车上有接收装置，总质量M2=2kg，问：甲车至少以多大的水平速度将小球发射到乙车上，两车才会相撞？(球最终停在乙车上)
一列简谐横波，在t=0时刻的波形如图所示，质点振动的振幅为10cm。P、Q两点的坐标分别为-1m和-9m，波传播方向由右向左，已知t=0.7s时, P点第二次出现波峰。试计算：
①这列波的传传播速度多大？
②从t=0时刻起，经多长时间Q点第一次出现波峰？
③当Q点第一次出现波峰时，P点通过的路程为多少？
粤公网安备 44130202000953号