如图，在竖直平面内有一固定光滑轨道，其中AB是长为R的水平直轨道，BCD是圆心为O、半径为R的3/4圆弧轨道，两轨道相切于B点。在外力作用下，一小球从A点由静止开始做匀加速直线运动，到达B点时撤除外力。已知小球经过最高点C时对轨道有向上的压力为mg/4，重力加速度为g。求：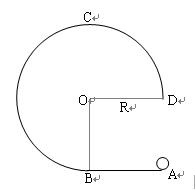
（1）小球在最高点C的速度；
（2）小球在AB段运动的加速度大小；
（3）小球从D点运动到A点所用的时间。
一个带正电的粒子，从A点射入水平方向的匀强电场中，粒子沿直线AB运动，如图所示。已知AB与电场线夹角θ＝45°，带电粒子的质量m＝1.0×10－7 kg，电荷量q＝1.0×10－10C，A、B相距L＝20 cm。（取g＝10 m/s2） 试判断带电粒子在电场中做怎样的运动，并求电场强度的大小和方向。
把两个带电小球Q1、Q2分别放在真空中的A、B两点。已知Q1=4.0×10-10C，Q2=-6.0×10-12C，r = 50cm，如图所示。
（1）求Q2受到的静电力的大小和方向。
（2）求Q1在B点产生的电场强度的大小和方向。
某同学在做测定电源的电动势和内电阻的实验中，用同一套器材采用如图中甲、乙所示的两种不同电路进行测量，并在同一坐标系中作出了两次测定的U-I图线如图中丙图所示，图中的C点与A点很接近.试问：
(1)图线AB是按哪种电路的测量作出的
(2)电池的电动势、内电阻的真实值是多少
(3)电流表的内阻是多少
下图所示的电路中，电源的电动势E="6.0" V，内电阻r="1.0" Ω，外电路的电阻R="5.0" Ω.闭合开关S,求：
（1）通过电阻R的电流；
（2）电阻R消耗的电功率.
如图所示，匀强磁场B 1 垂直水平光滑金属导轨平面向下，垂直导轨放置的导体棒ab在平行于导轨的外力F作用下做匀加速直线运动，通过两线圈感应出电压，使电压表示数U保持不变。已知变阻器最大阻值为R，且是定值电阻R 2 的三倍，平行金属板MN相距为d。在电场作用下，一个带正电粒子从O 1 由静止开始经O 2 小孔垂直AC边射入第二个匀强磁场区，该磁场的磁感应强度为B 2 ，方向垂直纸面向外，其下边界AD距O 1 O 2 连线的距离为h。已知场强B 2 =B，设带电粒子的电荷量为q、质量为m，则高度 
，请注意两线圈绕法，不计粒子重力。求：
（1）试判断拉力F能否为恒力以及F的方向（直接判断）；
（2）调节变阻器R的滑动头位于最右端时，MN两板间电场强度多大？
（3）保持电压表示数U不变，调节R的滑动头，带电粒子进入磁场B 2 后都能击中AD边界，求粒子打在AD边界上的落点距A点的距离范围。
粤公网安备 44130202000953号