(13分)如图所示,用完全相同的、劲度系数均为k的轻弹簧A、B、C将两个质量均为m的小球连接并悬挂起来,两小球均处于静止状态,弹簧A与竖直方向的夹角为30°,弹簧C水平,已知重力加速度为g,试求出轻弹簧A、B、C各自的伸长量。(所有弹簧形变均在弹性范围内)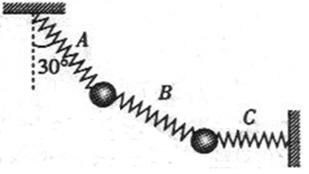
(13分)如图所示,用完全相同的、劲度系数均为k的轻弹簧A、B、C将两个质量均为m的小球连接并悬挂起来,两小球均处于静止状态,弹簧A与竖直方向的夹角为30°,弹簧C水平,已知重力加速度为g,试求出轻弹簧A、B、C各自的伸长量。(所有弹簧形变均在弹性范围内)