如图所示，足够长的U型光滑导体框架的两个平行导轨间距为L，导轨间连有定值电阻R，框架平面与水平面之间的夹角为θ，不计导体框架的电阻．整个装置处于匀强磁场中，磁场方向垂直于框架平面向上，磁感应强度大小为B 。导体棒ab的质量为m，电阻不计，垂直放在导轨上并由静止释放，重力加速度为g.求：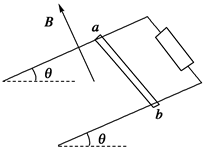
(1)导体棒ab下滑的最大速度；
(2)导体棒ab以最大速度下滑时定值电阻消耗的电功率。
相关试题
小车托着穿过打点计时器的纸带做匀变速直线运动，如图是经打点计时器打出的纸带的一段，计数点序号（按打点顺序计数）是A、B、C、D…….,以已知交流电的频率为50Hz,纸带上每相邻两个计数点间还有四个计时点。则小车的加速度大小是______
，小车做_______运动（填“匀速”、“匀加速”或“匀减速”）。当打点计时器打A点时，小车速度为_______m/s(保留三位有效数字) 
(本题10分)如图所示，一质量m=2kg的木块静止于水平地面上。现对物体施加一大小为10N的水平方向拉力。
(1)若地面光滑，求物体运动的加速度大小；
(2)若物体与地面间动摩擦因数μ=0.1，求物体的加速度大小和经过2s物体的位移大小。 (g=10 m/s2)
如图所示，质量为m =10kg的物体，在F=60N水平向右的拉力作用下，由静止开始运动。设物体与水平面之间的动摩擦因素µ=0.4，g=10m/s2求：
（1）物体所滑动受摩擦力为多大？（2）在拉力的作用下物体运动的加速度为多大？
粤公网安备 44130202000953号