2013年6月11日下午,神舟十号载人飞船进入近地点距地心为r1、远地点距地心为r2的椭圆轨道正常运行。已知地球质量为M,引力常量为G,地球表面处的重力加速度为g,飞船在近地点的速度为v1,飞船的质量为m。若取距地球无穷远处为引力势能零点,则距地心为r、质量为m的物体的引力势能表达式为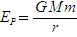 ,求:
,求:
(1)地球的半径;
(2)飞船在远地点的速度。
2013年6月11日下午,神舟十号载人飞船进入近地点距地心为r1、远地点距地心为r2的椭圆轨道正常运行。已知地球质量为M,引力常量为G,地球表面处的重力加速度为g,飞船在近地点的速度为v1,飞船的质量为m。若取距地球无穷远处为引力势能零点,则距地心为r、质量为m的物体的引力势能表达式为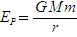 ,求:
,求:
(1)地球的半径;
(2)飞船在远地点的速度。