长L＝0.5 m、质量可忽略的杆，其一端固定于O点，另一端连有质量m＝2 kg的小球，它绕O点在竖直平面内做圆周运动．当通过最高点时，如图所示，求下列情况下，杆受到的力(计算出大小，并说明是拉力还是压力，g取10 m/s2)：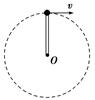
(1)当v＝1 m/s时，杆受到的力多大，是什么力？
(2)当v＝4 m/s时，杆受到的力多大，是什么力？
相关试题
桌面上有一玻璃圆锥，圆锥的轴（图中虚线）与桌面垂直，过轴线的截面为等边三角形，此三角形的边长为L，如图所示，有一半径为
的圆柱形平行光束垂直底面入射到圆锥上，光束的中心轴与圆锥的轴重合。已知玻璃的折射率为
，求：
①光在玻璃中的传播速度是多少？
②光束在桌面上形成的光斑的面积是多少？
如图所示，某复合光经过半圆形玻璃砖后分成a、b两束光，其中光束a与法线的夹角为60°，光束b与法线的夹角为45°，已知光在真空中的速度c=3.0×108m/s.则：
（1）a光在玻璃中的传播速度是多少？
（2）入射光绕O点逆时针至少再旋转多大角度就无折射光？
为测量一块等腰直角三棱镜
的折射率,用一束激光沿平行于BC边的方向射向直角边AB边,如图所示.激光束进入棱镜后射到另直角边AC边时,刚好能发生全反射.该棱镜的折射率为多少？
如图，为一圆柱中空玻璃管，管内径为R1，外径为R2，R2＝2R1.一束光线在圆柱横截面内射向玻璃管，为保证在内壁处光不会进入中空部分，问入射角i应满足什么条件？
，玻璃对该光的折射率为1.5，容器底部玻璃的厚度为d，水的深度也为d。
粤公网安备 44130202000953号