如图所示,质量M=1kg的木板静止在粗糙的水平地面上,木板与地面间的动摩擦因数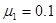 ,在木板的左端放置一个质量为m=1kg,大小可忽略的铁块,铁块与木板间的动摩擦因数
,在木板的左端放置一个质量为m=1kg,大小可忽略的铁块,铁块与木板间的动摩擦因数 ,取g=10m/s2,试求:
,取g=10m/s2,试求: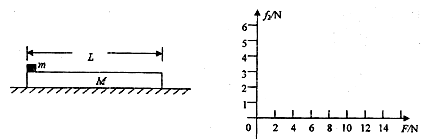
(1)若木板长L=1m,在铁块上加一个水平向右的恒力F=8N,经过多长时间铁块运动到木板右端
(2)若在铁块上加一个大小从零开始均匀增加的水平向右的力F,通过分析和计算后,请在图中画出铁块受到木板的摩擦力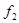 随拉力F大小变化的图像。(设木板足够长)
随拉力F大小变化的图像。(设木板足够长)
如图所示,质量M=1kg的木板静止在粗糙的水平地面上,木板与地面间的动摩擦因数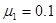 ,在木板的左端放置一个质量为m=1kg,大小可忽略的铁块,铁块与木板间的动摩擦因数
,在木板的左端放置一个质量为m=1kg,大小可忽略的铁块,铁块与木板间的动摩擦因数 ,取g=10m/s2,试求:
,取g=10m/s2,试求:
(1)若木板长L=1m,在铁块上加一个水平向右的恒力F=8N,经过多长时间铁块运动到木板右端
(2)若在铁块上加一个大小从零开始均匀增加的水平向右的力F,通过分析和计算后,请在图中画出铁块受到木板的摩擦力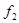 随拉力F大小变化的图像。(设木板足够长)
随拉力F大小变化的图像。(设木板足够长)