在距沙坑表面高h=8m处，以v0=22m/s的初速度竖直向上抛出一质量m=0.5kg的物体，物体落到沙坑并陷入沙坑d=0.3m深处停下。若物体在空中运动时的平均阻力是重力的0.1倍（g=10m/s2）。求：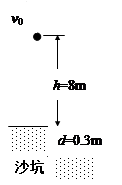
（1）物体上升到最高点时离开沙坑表面的高度H；
（2）物体在沙坑中受到的平均阻力F是多少？
相关试题
，追击一辆速度为
同向行驶的汽车，欲使投弹击中汽车，飞机应在距汽车水平距离多远处投弹？
如图所示，一绳系一球在光滑的桌面上做匀速圆周运动，绳长L＝0.1m，当角速度为 ω＝20πrad/s时，绳断开，试分析绳断开后：
(1) 小球在桌面上运动的速度；
(2) 若桌子高1m，小球离开桌子后运动的时间．
一平板车
，质量M=100kg，停在水平路面上，车身的平板离地面的高度h=1.25m，一质量m=50kg的小物块置于车的平板上，它到车尾端的距离b=1.00m，与车板间的滑动摩擦系数μ=0.20，如图所示．今对平板车施一水平方向的恒力，使车向前行驶，结果物块从车板上滑落．物块刚离开车板的时刻，车向前行驶的距离s0=2.0m。不计路面与平板车间以及轮轴之间
的摩擦．取g=10m/s2．求
（1）物块从车上滑落时物块的速度v1和平板车的速度v2
（2）物块从车上滑落到落地的时间t
（3）物块落地时，落地点到车尾的水平距离x．
粤公网安备 44130202000953号