如图所示,在倾角为θ的斜面上放置一内壁光滑的凹槽A,凹槽A与斜面间的动摩擦因数μ=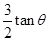 ,槽内紧靠右挡板处有一小物块B,它与凹槽左挡板的距离为d.A、B的质量均为m,斜面足够长.现同时由静止释放A、B,此后B与A挡板每次发生碰撞均交换速度,碰撞时间都极短.已知重力加速度为g.求:
,槽内紧靠右挡板处有一小物块B,它与凹槽左挡板的距离为d.A、B的质量均为m,斜面足够长.现同时由静止释放A、B,此后B与A挡板每次发生碰撞均交换速度,碰撞时间都极短.已知重力加速度为g.求: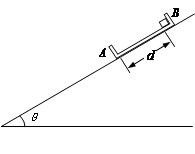
(1)物块B从开始释放到与凹槽A发生第一次碰撞所经过的时间t1.
(2)B与A发生第一次碰撞后,A下滑时的加速度大小aA和发生第二次碰撞前瞬间物块B的速度大小v2.
(3)凹槽A沿斜面下滑的总位移大小x.
如图所示,在倾角为θ的斜面上放置一内壁光滑的凹槽A,凹槽A与斜面间的动摩擦因数μ=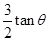 ,槽内紧靠右挡板处有一小物块B,它与凹槽左挡板的距离为d.A、B的质量均为m,斜面足够长.现同时由静止释放A、B,此后B与A挡板每次发生碰撞均交换速度,碰撞时间都极短.已知重力加速度为g.求:
,槽内紧靠右挡板处有一小物块B,它与凹槽左挡板的距离为d.A、B的质量均为m,斜面足够长.现同时由静止释放A、B,此后B与A挡板每次发生碰撞均交换速度,碰撞时间都极短.已知重力加速度为g.求:
(1)物块B从开始释放到与凹槽A发生第一次碰撞所经过的时间t1.
(2)B与A发生第一次碰撞后,A下滑时的加速度大小aA和发生第二次碰撞前瞬间物块B的速度大小v2.
(3)凹槽A沿斜面下滑的总位移大小x.