如图所示，位于竖直平面内的1/4 圆弧光滑轨道，半径为R，轨道的最低点B 的切线沿水平方向，轨道上端A 距水平地面高度为H．质量为m 的小球（可视为质点）从轨道最上端A 点由静止释放，经轨道最下端B 点水平飞出，最后落在水平地面上的C 点处，若空气阻力可忽略不计，重力加速度为g．求：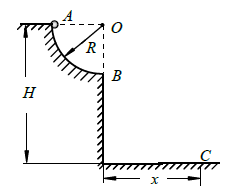 
（1）小球运动到B 点时，轨道对它的支持力；
（2）小球落地点C 与B 点的水平距离x；
（3）比值R/H 为多少时，小球落地点C 与B 点水平距离x 最远，及该最大水平距离．
如图所示，在水平地面上固定一倾角θ=37°、表面光滑且足够长的斜面体，物体A以v1=6m／s的初速度沿斜面上滑，同时在物体A的正上方，有一物体B以某一初速度水平抛出。如果当A上滑到最高点时恰好被B物体击中。(A、B均可看作质点，sin37°=0.6，cos37°=0.8。g 取10m／s²。)求：
（1）物体A上滑到最高点所用的时间t
（2）物体B抛出时的初速度
（3）物体A、B间初始位置的高度差h
火箭载着宇宙探测器飞向某行星，火箭内平台上还放有测试仪器，如图所示。火箭从地面起飞时，以加速度
竖直向上做匀加速直线运动(
为地面附近的重力加速度)，已知地球半径为R，升到某一高度时，测试仪器对平台的压力刚好是起飞时压力的
，求此时火箭离地面的高度h。
如图质量为m=0.2kg的小球固定在长为L=0.9m的轻杆一端，杆可绕O点的水平转轴在竖直平面内转动，g=10m/s2，求：
（1）小球在最高点的速度v1为多大时，球对杆的作用力为0？
（2）当小球在最高点的速度v2=6m/s时，球对杆的作用力和方向。
有一辆质量为800kg的小汽车驶上圆弧半径为50m的拱桥。
（1）汽车到达桥顶时速度为5m/s，汽车对桥的压力是多大？
（2）汽车以多大速度经过桥顶时恰好对桥没有压力而腾空？
粤公网安备 44130202000953号