如右图所示,竖直平面内两根光滑细杆所构成的角∠AOB被铅垂线OO′平分,∠AOB=120°.两个质量均为m的小环P、Q通过水平轻弹簧的作用静止在A、B两处,A、B连线与OO′垂直,连线与O点的距离为h,弹簧原长为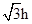 .现在两小环沿杆向下移动至A′B′,使其在竖直方向上均下移h距离,同时释放两环.整个过程未超出弹簧的弹性限度,重力加速度为g,试求:
.现在两小环沿杆向下移动至A′B′,使其在竖直方向上均下移h距离,同时释放两环.整个过程未超出弹簧的弹性限度,重力加速度为g,试求:
(1)弹簧的劲度系数;
(2)释放瞬间两环加速度的大小.
如右图所示,竖直平面内两根光滑细杆所构成的角∠AOB被铅垂线OO′平分,∠AOB=120°.两个质量均为m的小环P、Q通过水平轻弹簧的作用静止在A、B两处,A、B连线与OO′垂直,连线与O点的距离为h,弹簧原长为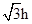 .现在两小环沿杆向下移动至A′B′,使其在竖直方向上均下移h距离,同时释放两环.整个过程未超出弹簧的弹性限度,重力加速度为g,试求:
.现在两小环沿杆向下移动至A′B′,使其在竖直方向上均下移h距离,同时释放两环.整个过程未超出弹簧的弹性限度,重力加速度为g,试求:
(1)弹簧的劲度系数;
(2)释放瞬间两环加速度的大小.