如图所示,质量0.1kg的小球.从光滑轨道顶端滚下,圆轨道半径R=0.5m.小球经过A和B时,速度分别为VA=4m/s和VB="8m/s" .设g=1 0m／s2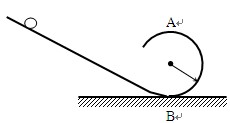
(1)计算小球在A时具有的重力势能(取B处为零势能)
(2)计算小球由B到达A时克服摩擦力所做的功
相关试题
如图9所示，将质量mA＝100 g的平台A连接在劲度系数k＝200 N/m的弹簧上端，形成竖直方向的弹簧振子，在A的上方放置mB＝mA的物块B，使A、B一起上下振动．若弹簧原长为5 cm，求：
图9
(1)当系统进行小振幅振动时，平衡位置离地面C的高度；
(2)当振幅为0.5 cm时，B对A的最大压力；
(3)为使B在振动中始终与A接触，振幅不得超过多少？
如图8所示为A、B两个简谐运动的位移—时间图象．
图8
试根据图象写出：
(1)A的振幅是______cm，周期是________s；B的振幅是________cm，周期是________s.
(2)这两个简谐运动的位移随时间变化的关系式．
(3)在时间t＝0.05 s时两质点的位移分别是多少？
如图16所示，简谐运动的图象上有a、b、c、d、e、f六个点，其中
图16
(1)与a位移相同的点有哪些？
(2)与a速度相同的点有哪些？
(3)b点离开平衡位置的最大距离有多大？
粤公网安备 44130202000953号