(1)开普勒行星运动第三定律指出:行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比,即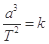 ,k是一个对所有行星都相同的常量.将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式.已知引力常量为G,太阳的质量为M太.
,k是一个对所有行星都相同的常量.将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式.已知引力常量为G,太阳的质量为M太.
(2) 一均匀球体以角速度ω绕自己的对称轴自转,若维持球体不被瓦解的唯一作用力是万有引力,则此球的最小密度是多少?
(1)开普勒行星运动第三定律指出:行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比,即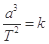 ,k是一个对所有行星都相同的常量.将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式.已知引力常量为G,太阳的质量为M太.
,k是一个对所有行星都相同的常量.将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式.已知引力常量为G,太阳的质量为M太.
(2) 一均匀球体以角速度ω绕自己的对称轴自转,若维持球体不被瓦解的唯一作用力是万有引力,则此球的最小密度是多少?