如图所示,在匀强磁场中有一个“n”形导线框可绕AB轴转动,已知匀强磁场的磁感应强度B=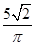 T(磁场无限大),线框的CD边长为l1=20 cm,CE、DF边长均为l2=10 cm,线圈电阻r=1 Ω,转速为50 r/s. 外电路电阻R=4 Ω,若从图示位置开始计时,
T(磁场无限大),线框的CD边长为l1=20 cm,CE、DF边长均为l2=10 cm,线圈电阻r=1 Ω,转速为50 r/s. 外电路电阻R=4 Ω,若从图示位置开始计时,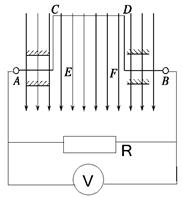
(1)转动过程中感应电动势的最大值;
(2)由图示位置(线圈平面与磁感线平行)转过60°角时的瞬时感应电动势;
(3)交流电压表的示数;
(4) 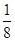 周期内通过R的电荷量为多少?
周期内通过R的电荷量为多少?
相关知识点
如图所示,在匀强磁场中有一个“n”形导线框可绕AB轴转动,已知匀强磁场的磁感应强度B=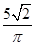 T(磁场无限大),线框的CD边长为l1=20 cm,CE、DF边长均为l2=10 cm,线圈电阻r=1 Ω,转速为50 r/s. 外电路电阻R=4 Ω,若从图示位置开始计时,
T(磁场无限大),线框的CD边长为l1=20 cm,CE、DF边长均为l2=10 cm,线圈电阻r=1 Ω,转速为50 r/s. 外电路电阻R=4 Ω,若从图示位置开始计时,
(1)转动过程中感应电动势的最大值;
(2)由图示位置(线圈平面与磁感线平行)转过60°角时的瞬时感应电动势;
(3)交流电压表的示数;
(4) 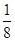 周期内通过R的电荷量为多少?
周期内通过R的电荷量为多少?