如图所示，长为R的不可伸长轻绳上端固定在O点，下端连接一小球，小球与地面间的距离可以忽略（但小球不受地面支持力）且处于静止状态．在最低点给小球一沿水平方向的初速度，此时绳子恰好没断，小球在竖直平面内做圆周运动。假设小球到达最高点时由于绳子碰到正下方P处的钉子恰好断裂，最后小球落在距初始位置水平距离为4R的地面上，重力加速度为g．试求：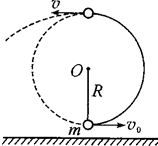 
(1)绳突然断开时小球的速度v；
(2)竖直方向上O与P的距离L．
光子具有能量，也具有动量。光照射到物体表面时，会对物体产生压强，这就是“光压”。光压的产生机理如同气体压强：大量气体分子与器壁的频繁碰撞产生了持续均匀的压力，器壁在单位面积上受到的压力就是气体的压强。设太阳光每个光子的平均能量为E，太阳光垂直照射地球表面时，在单位面积上的辐射功率为P0。已知光速为c，则光子的动量为E/c。求：
（1）若太阳光垂直照射在地球表面，则时间t内照射到地球表面上半径为r的圆形区域内太阳光的总能量及光子个数分别是多少？
（2）若太阳光垂直照射到地球表面，在半径为r的某圆形区域内被完全反射（即所有光子均被反射，且被反射前后的能量变化可忽略不计），则太阳光在该区域表面产生的光压（用I表示光压）是多少？
（3）有科学家建议利用光压对太阳帆的作用作为未来星际旅行的动力来源。一般情况下，太阳光照射到物体表面时，一部分会被反射，还有一部分被吸收。若物体表面的反射系数为ρ，则在物体表面产生的光压是全反射时产生光压的
倍。设太阳帆的反射系数ρ=0.8，太阳帆为圆盘形，其半径r=15m，飞船的总质量m=100kg，太阳光垂直照射在太阳帆表面单位面积上的辐射功率P0=1.4kW，已知光速c=3.0×108m/s。利用上述数据并结合第（2）问中的结论，求太阳帆飞船仅在上述光压的作用下，能产生的加速度大小是多少?不考虑光子被反射前后的能量变化。（保留2位有效数字）
发电站通过升压变压器、输电导线和降压变压器把电能输送到用户,如果升压变压器和降压变压器都可视为理想变压器.
（1）画出上述输电全过程的线路图.
（2）若发电机的输出功率是 100 kW,输出电压是250 V,升压变压器的原、副线圈的匝数比为 1∶25,求升压变压器的输出电压和输电导线中的电流.
（3）若输电导线中的电功率损失为输入功率的 4%,求输电导线的总电阻和降压变压器原线圈两端的电压.
（4）计算降压变压器的输出功率.
在其他能源中，核能具有能量密度大、地区适应性强的优势.在核电站中，核反应堆释放的核能被转化为电能.核反应堆的工作原理是利用中子轰击重核发生裂变反应，释放出大量核能.
（1）核反应方程式
+n→
+
+aX是反应堆中发生的许多核反应中的一种，n为中子，X为待求粒子，a为X的个数，则X为______，a=______.以mU、mBa、mKr分别表示、、的质量.mn、mp分别表示中子、质子的质量，c为光在真空中传播的速度，则在上述反应过程中放出的核能ΔE=__________________________.
（2）有一座发电能力为P=1.00×106 kW的核电站，核能转化为电能的效率η=40%.假定反应堆中发生的裂变反应全是本题（1）中的核反应，已知每次核反应过程放出的核能ΔE=2.78×10－11 J,的质量mU=390×10－27 kg.求每年（1年=3.15×107 s）消耗的的质量.
如图所示，AB是粗糙的
圆弧，半径为R，OA水平，OB竖直，O点离地面高度为2R，一质量为m的小球，从A点静止释放，不计空气阻力，最后落在距C点R处的D点。
求：（1）小球经过B点时，对轨道的压力？
（2）小球在AB段克服阻力做的功？
粤公网安备 44130202000953号