如下左图所示,一个上下都与大气相通的直圆筒,内部横截面的面积S=0.01m2,中间用两个活塞A与B封住一定质量的理想气体,A、B都可沿圆筒无摩擦地上、下滑动,但不漏气,A的质量可不计、B的质量为M,并与一倔强系数k=5×103N/m的较长的弹簧相连。已知大气压强p0=1×105Pa,平衡时,两活塞间的距离l0=0.6m。现用力压A,使之缓慢向下移动一定距离后,保持平衡。此时,用于压A的力F=500N。求活塞A向下移的距离。(假定气体温度保持不变。)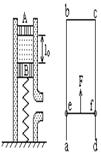
如下左图所示,一个上下都与大气相通的直圆筒,内部横截面的面积S=0.01m2,中间用两个活塞A与B封住一定质量的理想气体,A、B都可沿圆筒无摩擦地上、下滑动,但不漏气,A的质量可不计、B的质量为M,并与一倔强系数k=5×103N/m的较长的弹簧相连。已知大气压强p0=1×105Pa,平衡时,两活塞间的距离l0=0.6m。现用力压A,使之缓慢向下移动一定距离后,保持平衡。此时,用于压A的力F=500N。求活塞A向下移的距离。(假定气体温度保持不变。)