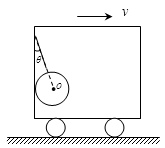
如图所示，质量为4kg的小球用轻质细绳拴着吊在行驶的汽车后壁上。细绳的延长线通过小球的球心O，且与竖直方向的夹角为θ=37º。g取10 m/s2，已知sin37º=0.6，cos37º=0.8，求：
（1）汽车匀速运动时，细线对小球的拉力和车后壁对小球的压力；
（2）若要始终保持θ=37º，则汽车刹车时的加速度最大不能超过多少。
如图所示，质量的滑块套在光滑的水平轨道上，质量
的小球通过长
的轻质细杆与滑块上的光滑轴
连接，小球和轻杆可在竖直平面内绕
轴自由转动，开始轻杆处于水平状态，现给小球一个竖直向上的初速度
，
取
。
（1）若锁定滑块，试求小球通过最高点时对轻杆的作用力大小和方向。
（2）若解除对滑块的锁定，试求小球通过最高点时的速度大小。
（3）在满足（2）的条件下，试求小球击中滑块右侧轨道位置点与小球起始位置点间的距离。
如图甲，在的空间中存在沿
轴负方向的匀强电场和垂直于
平面向里的匀强磁场，电场强度大小为
，磁感应强度大小为
。一质量为
，带电量为
的粒子从坐标原点
处，以初速度
沿
轴正方向射入，粒子的运动轨迹见图甲，不计粒子的重力。
⑴求该粒子运动到时的速度大小
；
⑵现只改变入射粒子初速度的大小，发现初速度大小不同的粒子虽然运动轨迹（曲线）不同，但具有相同的空间周期性，如图乙所示；同时，这些粒子在
轴方向上的运动（
关系）是简谐运动，且都有相同的周期
。
Ⅰ．求粒子在一个周期内，沿
轴方向前进的距离
；
Ⅱ．当入射粒子的初速度大小为时，其
图像如图丙所示，求该粒子在
轴方向上做简谐运动的振幅
，并写出
的函数表达式。
如图为某种鱼饵自动投放器中的投饵管装置示意图，其下半部AB是一长为2的竖直细管，上半部
是半径为
的四分之一圆弧弯管，管口沿水平方向，
管内有一原长为
、下端固定的轻质弹簧。投饵时，每次总将弹簧长度压缩到0.5
后锁定，在弹簧上端放置一粒鱼饵，解除锁定，弹簧可将鱼饵弹射出去。设质量为
的鱼饵到达管口
时，对管壁的作用力恰好为零。不计鱼饵在运动过程中的机械能损失，且锁定和解除锁定时，均不改变弹簧的弹性势能。已知重力加速度为
。求：
（1）质量为的鱼饵到达管口
时的速度大小
；
（2）弹簧压缩到0.5时的弹性势能
；
（3）已知地面与水面相距1.5，若使该投饵管绕AB管的中轴线
在90º角的范围内来回缓慢转动，每次弹射时只放置一粒鱼饵，鱼饵的质量在2
到3
之间变化，且均能落到水面。持续投放足够长时间后，鱼饵能够落到水面的最大面积
是多少？
反射式速调管是常用的微波器件之一，它利用电子团在电场中的振荡来产生微波，其振荡原理与下述过程类似。如图所示，在虚线两侧分别存在着方向相反的两个匀强电场，一带电微粒从
点由静止开始，在电场力作用下沿直线在
、
两点间往返运动。已知电场强度的大小分别是
和
，方向如图所示。带电微粒质量
，带电量
，
点距虚线
的距离
，不计带电微粒的重力，忽略相对论效应。求：
⑴点到虚线
的距离
；
⑵带电微粒从点运动到
点所经历的时间
。
粤公网安备 44130202000953号