如图所示,水平绝缘轨道 与处于竖直平面内的半圆形绝缘光滑轨道
与处于竖直平面内的半圆形绝缘光滑轨道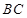 平滑连接,半圆形轨道的半径
平滑连接,半圆形轨道的半径 。轨道所在空间存在水平向右的匀强电场,电场强度
。轨道所在空间存在水平向右的匀强电场,电场强度 。现有一电荷量
。现有一电荷量 ,质量
,质量 的带电体(可视为质点),在水平轨道上的
的带电体(可视为质点),在水平轨道上的 点由静止释放,已知
点由静止释放,已知 点与圆形轨道最低点
点与圆形轨道最低点 距离
距离 .带电体与水平轨道间的动摩擦因数
.带电体与水平轨道间的动摩擦因数 ,重力加速度
,重力加速度 ,取
,取 .求:
.求:
(1)带电体运动到圆形轨道的最高点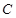 时,速度的大小?
时,速度的大小?
(2)带电体第一次经过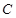 点后,落在水平轨道上的位置到
点后,落在水平轨道上的位置到 点的距离?
点的距离?
(3)带电体在轨道上运动对轨道能产生的最大压力大小?
如图所示,水平绝缘轨道 与处于竖直平面内的半圆形绝缘光滑轨道
与处于竖直平面内的半圆形绝缘光滑轨道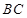 平滑连接,半圆形轨道的半径
平滑连接,半圆形轨道的半径 。轨道所在空间存在水平向右的匀强电场,电场强度
。轨道所在空间存在水平向右的匀强电场,电场强度 。现有一电荷量
。现有一电荷量 ,质量
,质量 的带电体(可视为质点),在水平轨道上的
的带电体(可视为质点),在水平轨道上的 点由静止释放,已知
点由静止释放,已知 点与圆形轨道最低点
点与圆形轨道最低点 距离
距离 .带电体与水平轨道间的动摩擦因数
.带电体与水平轨道间的动摩擦因数 ,重力加速度
,重力加速度 ,取
,取 .求:
.求:
(1)带电体运动到圆形轨道的最高点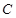 时,速度的大小?
时,速度的大小?
(2)带电体第一次经过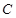 点后,落在水平轨道上的位置到
点后,落在水平轨道上的位置到 点的距离?
点的距离?
(3)带电体在轨道上运动对轨道能产生的最大压力大小?