带电小球的质量为m,当匀强电场方向水平向右时(图中未画出),小球恰能静止在光滑圆槽形轨道的A点,图中角θ=30°,如图所示,当将电场方向转为竖直向下时(保持匀强电场的电场强度大小不变),求小球从A点起滑到最低点时对轨道的压力.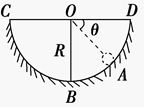
相关知识点
带电小球的质量为m,当匀强电场方向水平向右时(图中未画出),小球恰能静止在光滑圆槽形轨道的A点,图中角θ=30°,如图所示,当将电场方向转为竖直向下时(保持匀强电场的电场强度大小不变),求小球从A点起滑到最低点时对轨道的压力.